definition of a Laplace transform
y(t)
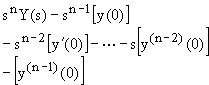
nth derivative
![]()
integration
![]()
f(t) has period T, such that
f( t + T ) = f (t)
g(t) has period T, such that
g(t + T ) = - g(t)
How It Works... |
Evaluating "how it works" requires that you apply a simple sequence of formulae readily understood by any 8-th grade pre-algebra student. Those formulae are presented below; To evaluate, set up the initial matrix by evaluating the first table of formulae in order. Then, for each resulting data point, evaluate using the second table of formulae (again, in order). |
For those without the elemental but requisite math background, a simple layman's explanation can be seen by clicking the link below:: |
|
|
|
|
|
| 1.1 | |
definition of a Laplace transform y(t) |
| 1.2 | Y(s) | inversion formula |
| 1.3 | |
first derivative |
| 1.4 | |
second derivative |
| 1.5 | 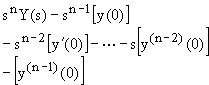 |
nth derivative
|
| 1.6 | |
integration
|
| 1.7 | F(s)G(s) | convolution integral |
| 1.8 | |
|
| 1.9 | |
shifting in the s-plane |
| 1.10 | |
f(t) has period T, such that f( t + T ) = f (t) |
| 1.11 | |
g(t) has period T, such that g(t + T ) = - g(t) |
|
|
|
|
|
|
|
1 |
unit impulse at t = 0 |
|
|
s |
double impulse at t = 0 |
|
|
|
|
|
|
|
unit step u(t) |
|
|
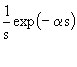 |
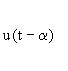 |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
the Gamma function is given in Appendix A |
|
|
|
|
|
|
|
|
| 2.11 | |
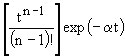 |
| 2.12 | |
|
| 2.13 | |
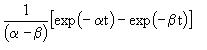 |
| 2.14 | |
|
| 2.15 | 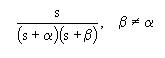 |
|
| 2.16a | |
|
| 2.16b | |
|
| 2.17 | |
|
| 2.18 |
|
|
| 2.19 | |
|
| 2.20 | 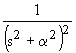 |
|
| 2.21 | 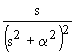 |
|
| 2.22 | 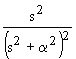 |
|
| 2.23 | |
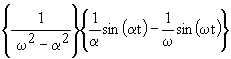 |
| 2.24 | |
|
| 2.25 | |
|
| 2.26 | |
|
| 2.27 | |
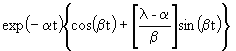 |
| 2.28 | |
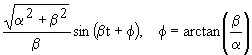 |
| 2.29 | |
|
| 2.30 | |
|
| 2.31 | |
|
| 2.32 | |
|
| 2.33 | |
|
| 2.34 | |